Recursive Functions
Contents
- Introduction
- Terminology
- Common Recursive Functions
- Ways of Evaluating Recursive Calls
- A Note on Efficiency
- Sample Problems
Introduction
As we probably know, functions are an essential part of programming; they allow us to get values, work with object data, and so many other things. Everyone should be familiar with normal functions that may have loops but ultimately comes to an end. However, recursive functions call on themselves in their own function.
Recursive functions are important because while all iterative functions can be written recursively (although efficiency-wise that may not always be the best), not all recursive functions can be written iteratively.
ACSL focuses more on mathematical recursive functions than programming algorithms, but we will cover both on this page.
Terminology
When it comes to recursive functions, there always has to be a defined endpoint; you wouldn't want your function to call on itself forever, after all! So, what you would need is at least one base case. For a base case, the function is not called on again; instead, a set value is returned. Here's an example (from online):
int pow_recursion(int x, int y) {
if (y < 0) {
return -1;
} else if (y == 0) {
return 1;
}
return pow_recursion(x, y - 1) * x;
}
Here, the two if conditions both represent a base case; when y is a certain value, then the
function will no longer continue to call on itself and will instead return a constant value.
Now, let's discuss a few "types" of recursion.
Indirection recursion is when function A calls on another function, function B, which eventually calls on function A again.
Single recursion is recursion that only calls on itself once in the function, an example being
the pow_recursion function mentioned previously.
Multiple recursion is when a function references itself multiple times; an example is the Fibonacci sequence referenced in the next section.
Infinite recursion is a recursive function that never stops because it keeps on calling itself.
A program with infinite recursion would eventually crash with a stack overflow error
message. Why this occurs may be a bit difficult to explain now, but we will come back to it in the
Ways of Evaluating Recursive Calls section.
Common Recursive Functions
Fibonacci Numbers
The Fibonacci sequence is a famous sequence that goes like so:
The first two numbers in the sequence are 0 and 1 respectively. After that, every number is the
sum of the preceding two numbers. So, the third number would be $0+1=1$. The fourth number
would be $1+1=2$.
So, overall, the list is 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, etc.
Now, how would be written as a function? First, we can establish that the base cases would be
$f(0) = 0$ and $f(1) = 1$. As a mathematical function, we can write:
$\begin{equation*}f(n) = \begin{cases}n &\text{if $n \leq 1$}\\f(n-1)+f(n-2) &\text{if $n > 1$}\end{cases}\end{equation*}$
If this was implemented as a programming function, it would be:
public static int fibonacci(int x) {
if(x <= 1) {
return x;
}
return fibonacci(x - 1) + fibonacci(x - 2);
}
Here's the Python version of the function if you'd like:
def fibonacci(x):
if x <= 1:
return x
return fibonacci(x - 1) + fibonacci(x - 2)
Factorials
Factorials can be written as $n!$, which equals $n \bullet (n - 1) \; \bullet \; ... \; \bullet \; 1$.
$0!$ would automatically have a value of 1. We will not worry about factorials of negative
numbers.
So, as a mathematical function, this can be written as:
$\begin{equation*}f(n) = \begin{cases}1 &\text{if $n = 0$}\\n \bullet f(n-1) &\text{if $n > 0$}\end{cases}\end{equation*}$
Then, here are the Java and Python implementations of this function:
public static int factorial(int x) {
if(x == 0) {
return 1;
}
return x * factorial(x - 1);
}
def factorial(x):
if x == 0:
return 1
return x * factorial(x - 1)
Ways of Evaluating Recursive Calls
There are three main ways of evaluating recursive calls: using stacks, drawing trees, or writing down equations. You can decide on which one you prefer the most. You can also develop your own methods if you would like.
(Approaches are most likely going to depend on the problem - i.e. you wouldn't use a tree if the function only recurred once per method call (i.e. single recursion), because then your tree would just be a downwards line.)
Stacks
This method is good for handling single recursion in the form of programming functions.
Here's an example:
public void mystery4(int nNum) {
if(nNum <= 0)
return;
mystery4(nNum - 1);
for(int nI = 0; nI < nNum; nI++) {
System.out.print("-");
}
for(int nI = 0; nI < nNum; nI++) {
System.out.print("+");
}
System.out.println();
}
Let's say we needed to evaluate what mystery4(4) would print. We can use a stack to model
each function call we make. Here's the process we can take:
| Step | Reasoning |
|---|---|
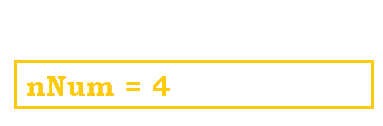 |
Our first call would of course be mystery4(4). So, we add this call to our stack. |
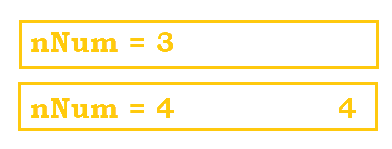 |
Since nNum is not less than or equal to zero, we skip over the base case and move to line 4, which is a recursive call. So, we add this recursive call to the stack. The extra 4 added to the bottom element marks what line in that specific function call that we left off at. |
 |
Here, we fast-forwarded and created the rest of the stack until we finally met the base case, nNum = 0. |
Now that the base case is reached, the real calculating can now begin.
| Step | Reasoning |
|---|---|
 |
Since nNum == 0, we return back to the previous function call, mystery4(1). Now that line 4 has been executed, we continue to execute the rest of the function starting from line 5. Based on the for loops, -+ would be printed and be followed by a new line. |
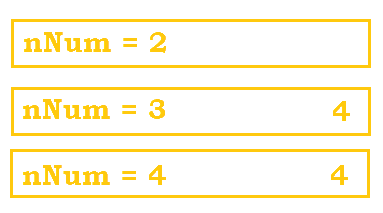 |
Now that we have finished executing the rest of mystery4(1), that is removed from the stack, and we move to mystery4(2). The same idea applies; we execute the rest of the function starting from line 5 and print out --++ with a new line. |
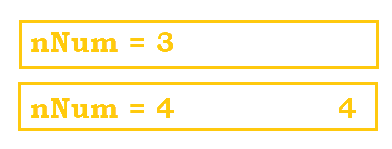 |
We move onto mystery4(3) and start from line 5. ---+++ is printed with a new line afterwards. |
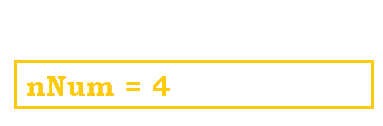 |
We are now onto the last element in our stack, mystery4(4), which was our original function. ----++++ is printed with a new line. |
So, ultimately, our final display from the call mystery4(4) gets us:
-+
--++
---+++
----++++
We can also use stacks to cover why you get a "stack overflow" error for infinite recursion. In the previous problem, we were able to stop stacking after we reached the base case and then work down the stack until there were no elements left.
However, in a program with infinite recursion, the computer would keep stacking and stacking method calls on the stack until eventually the call stack exceeds the stack bound (typically defined by the program upon startup), and the stack literally overflows.
Trees
This method is handy for dealing with multiple recursion. The Fibonacci sequence is a good example. Let's refer back to this equation:
$\begin{equation*}f(n) = \begin{cases}n &\text{if $n \leq 1$}\\f(n-1)+f(n-2) &\text{if $n > 1$}\end{cases}\end{equation*}$
Now, let's say we need to determine fibonacci(5). Here's how we could break down the
calculations.
| Step | Explanation |
|---|---|
 |
This is our original call, fibonacci(5). This will be the root of our tree. |
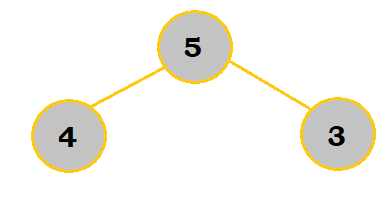 |
Since fibonacci(5) doesn't meet the base condition of N <= 1, we will have to make two recursive calls. This is represented by drawing two children from the 5 node. The 4 and 3 represent the new value for N in the recursive calls. |
Eventually, we would end up with this tree:
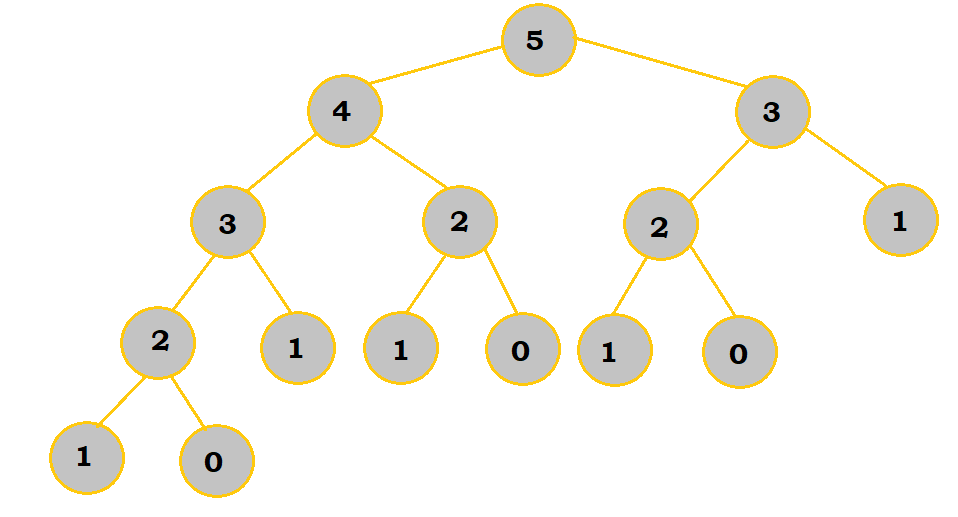
Notice how the ends of the tree all meet the base case; that is how you will know for sure that your tree has been fully constructed.
Now, you just need to work your way up for calculations. Here's how it would look like:
| Step | Explanation |
|---|---|
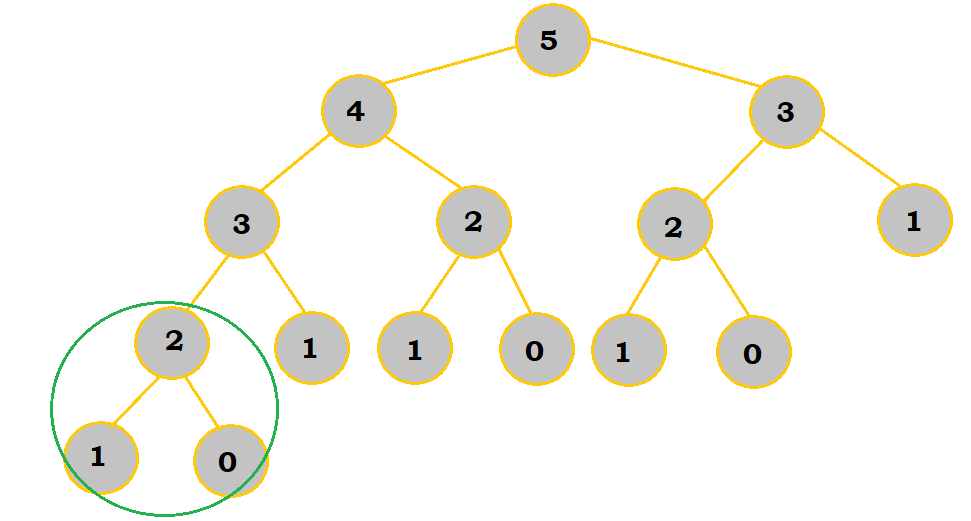 |
First, $fibonacci(1) = 1$ and $fibonacci(0) = 0$. $fibonacci(2) = fibonacci(1) + fibonacci(0)$. So, $fibonacci(2) = 1 + 0 = 1$. |
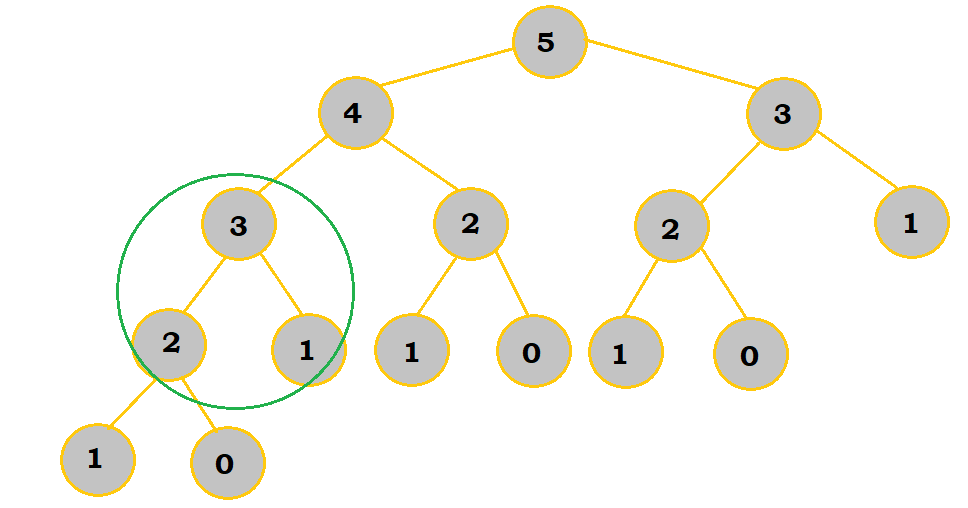 |
We have now determined that $fibonacci(2) = 1$. $fibonacci(1) = 1$ like before. $fibonacci(3) = fibonacci(2) + fibonacci(1) = 1 + 1 = 2$. |
Once you finish your calculations, you will end up with this:
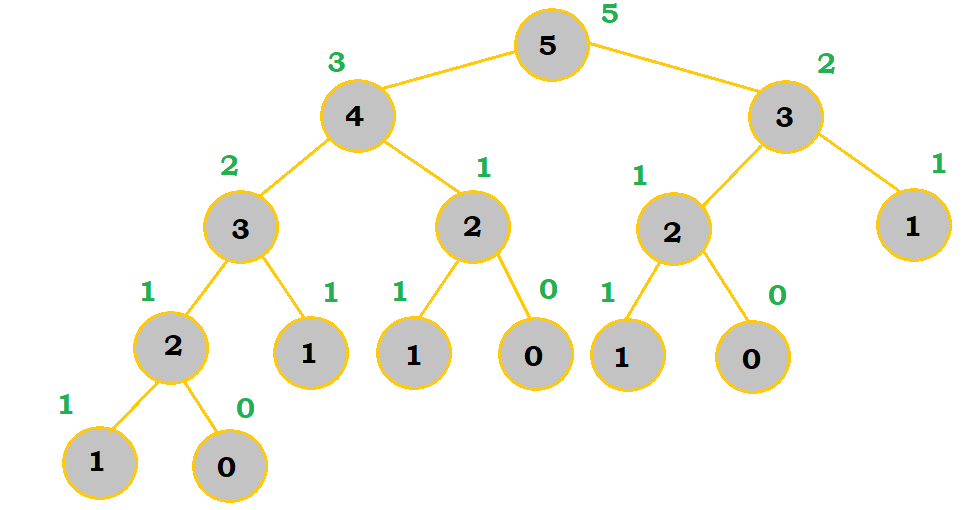
So, $fibonacci(5) = 5$.
Writing Equations
This method is good for handling mathematical functions. On the ACSL contests, you'll most likely be using this method because ACSL recursion problems are pretty much always written at mathematical functions rather than actual programming.
Sample Problem 1 on the ACSL Wiki page is a good example:
$\begin{equation*}g(x) = \begin{cases}g(x-3) + 1 &\text{if $x > 0$}\\3x &\text{if $x \leq 0$}\end{cases}\end{equation*}$
If we were to find the value of g(11), then we can write a series of equations.
$g(11) = g(11-3) + 1 = g(8) + 1$
$g(8) = g(8-3) + 1 = g(5) + 1$
$g(5) = g(5-3) + 1 = g(2) + 1$
$g(2) = g(2-3) + 1 = g(-1) + 1$
$g(-1) = 3 \bullet -1 = -3$
Now that we have reached the base condition, we can work back up the equations:
$g(11) = g(8) + 1 = 0 + 1 = 1$
$g(8) = g(5) + 1 = -1 + 1 = 0$
$g(5) = g(2) + 1 = -2 + 1 = -1$
$g(2) = g(-1) + 1 = -3 + 1 = -2$
$g(-1) = 3 \bullet -1 = -3$
So $g(11) = 1$.
A Note on Efficiency
When it comes to recursion, it's actually incredibly inefficient in a lot of cases. For example, the Fibonacci recursion
would completely break down if you tried to find fibonacci(50) because of how many recursive calls it would have to make.
In general, in your actual coding, you should try to avoid recursion if you can. However, understanding recursion is still a fundamental part of a greater understanding of programming - and there are a select few problems where recursion is the best (or even only) way to solve it.
The technique mainly used to avoid recursion is the very poorly named (in my opinion) dynamic programming. This often involves "memoization", which is the act of saving the results of previous calls ("memo"-izing them, like writing a memo) so that you don't have to recalculate them. This topic is honestly very complex and confusing, though it is one of the most important techniques in competitive programming - you will need it for USACO Gold contests and up, for example.
If you wish to learn more, that is well beyond the scope of this page, but there are many resources online that can help you.
Sample Problems
1. With the function below, determine the value of mystery(4).
public static int mystery(int num) {
if(num <= 0) {
return num;
} else {
return mystery(num - 1) + mystery(num - 3);
}
}
For this problem, I used the tree method. See how I set up the tree and determined the values along the way:
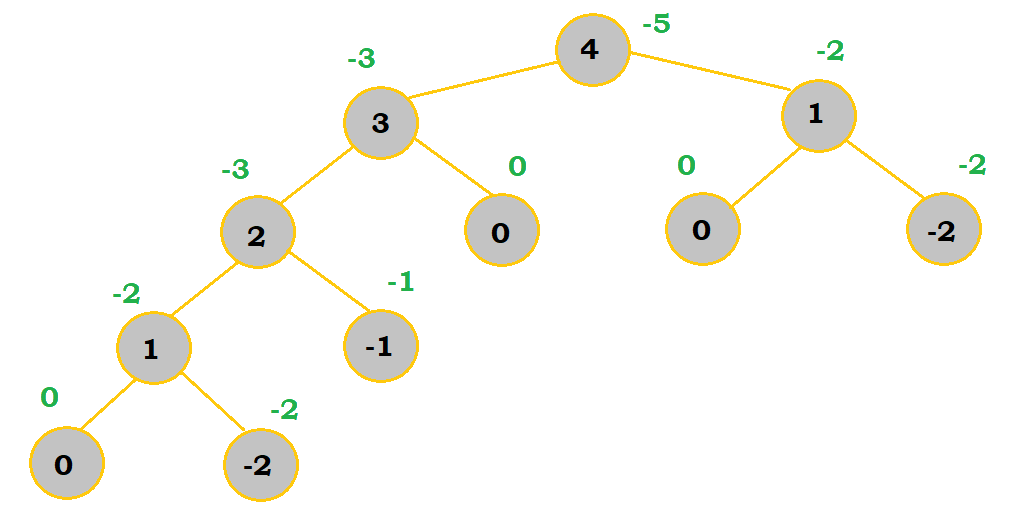
So, our final answer is -5.
2. With the mathematical function below, determine the value of f(6).
$\begin{equation*}f(x) = \begin{cases}f(x-15) &\text{if $x > 8$}\\f(f(x+7)-f(x+11)) &\text{if $3 \leq x \leq 8$}\\4x^2 &\text{if $x < 3$}\end{cases}\end{equation*}$
For this question, we will write equations to get our answer.
$f(6) = f(f(13)-f(17))$
$f(13) = f(-2)$
$f(17) = f(2)$
$f(-2) = 4 \bullet (-2)^2 = 16$
$f(2) = 4 \bullet 2^2 = 16$
Hence, $f(13) = f(17) = 16$.
$f(6) = f(16 - 16) = f(0)$.
$f(0) = 4 * 0^2 = 0$. So, our final answer is 0.
3. Find the value of f(17, 6) with the following mathematical function.
$\begin{equation*}f(x,y) = \begin{cases}f(x-y, y-1) + 2 &\text{if $x > y$}\\x + y &\text{if $x \leq y$}\end{cases}\end{equation*}$
We will also write equations to get our answer for this question.
$f(17, 6) = f(17 - 6, 6 - 1)+2 = f(11, 5) + 2$
$f(11, 5) = f(11 - 5, 5 - 1)+2 = f(6, 4) + 2$
$f(6, 4) = f(6 - 4, 4 - 1)+2 = f(2, 3) + 2$
$f(2, 3) = 2 + 3 = 5$
So, $f(6, 4) = 5 + 2 = 7$, $f(11, 5) = 7 + 2 = 9$, and $f(17, 6) = 9 + 2 = 11$. So, our
answer is 11.
4. If the following algorithm is applied to a square with a side of 16 feet, how many square feet will be painted?:
(Note: This is from the ACSL Wiki.)
- Given a square.
- If the length of a side is less than 2 feet, then stop.
- Divide the square into 4 equal size squares (i.e., draw a “plus” sign inside the square).
- Paint one of these 4 small squares.
- Repeat this procedure (start at step 1) for each of the 3 unpainted squares.
This problem gives you a glance at a pseudocode, non-mathematical or programming-related recursive algorithm.
Don't bother writing out a mathematical or programming function (unless you really want to). Instead, just follow the steps like you would if you were trying to build IKEA furniture or a LEGO set.
| Step | Image | Explanation |
|---|---|---|
| 1 | 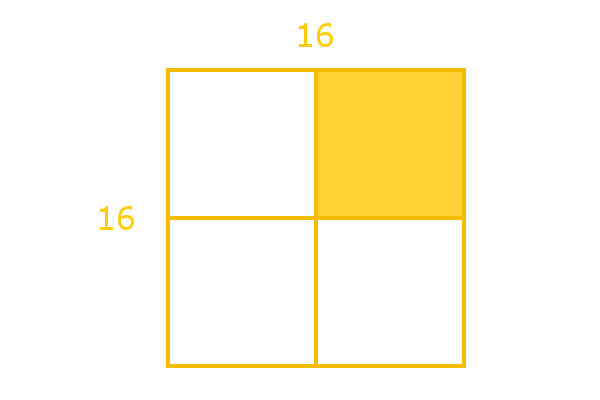 |
We first execute the algorithm on our original 16-foot square. We skip Step 2 because the condition doesn't apply. We then execute Steps 3-4. |
| 2 | 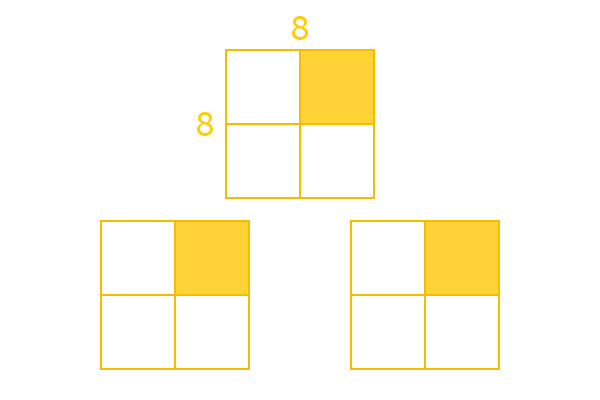 |
We will now execute Step 5 from our algorithm pass above. Again, Step 2 would be skipped here. So, we split each of these squares into 4 and paint one of the small squares. |
| 3 | 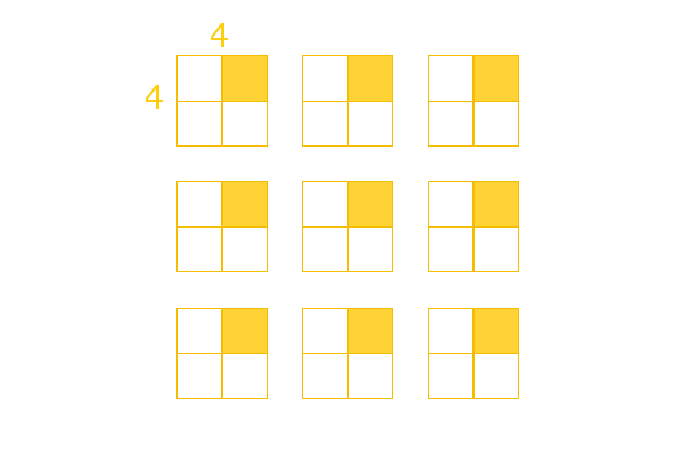 |
We continue the recursive process. Step 2 does not apply, so we divide and paint. |
| 4 |  |
Again, we go through another recursive pass. Divide and paint. |
When we apply the function again to the 81 small, unpainted squares, these squares will have only have a side length of 1 foot. Thus, instead of dividing further, we just stop here.
So, the last step is finding the number of square feet painted. In Step 1, we had one 8 x 8 square. In Step 2, we had three 4 x 4 squares. In Step 3, we had nine 2 x 2 squares. In Step 4, we had twenty-seven 1 x 1 squares.
So, we have $(1 * 8^2) + (3 * 4^2) +
(9 * 2^2) + (27 * 1^2)$
$= 64 + 48 + 36 + 27 = 175$ square feet.
Author: Kelly Hong, Raymond Zhao