Pre-fix, Post-fix, and In-fix Notation
Contents
Introduction
We all come in contact with math in numerous situations. Whenever we see a math expression
like $8 + 14 * 6$, we are looking at infix notation. In-fix means that the operators (like $+$ or $*$)
are written between its two operands (the numbers the operation works with). However, there are two other notations that we
will explore next.
More Types of Notations
As we touched upon in the Introduction, we should all be very much acquainted with in-fix notation.
Another type of notation is pre-fix notation, where each operator is placed before
its operands. So, the pre-fix notation of $8 + 14 * 6$ would be $+ \;8 \;* \;14 \;6$.
The other type of notation is post-fix notation, where each operator is placed after
its operands instead. The post-fix notation of $8 + 14 * 6$ would be $8 \; 14 \; 6 * +$.
One note is that exponents are marked with a $\uparrow$ rather than a ^ mark.
Also, pre-fix and post-fix both do not use parentheses.
Evaluating Expressions in Any Notation
When it comes to evaluating in-fix expressions, you would simply follow PEMDAS: parentheses, exponents, multiplication, division, addition, and then subtraction. Multiplication and division have the same precedence, as do addition and subtraction; terms with equal precedence are evaluated from left to right.
With pre-fix and post-fix, there is no specific order of precedence.
For pre-fix, you would first scan the expression for any operators that are followed by 2 operands, simplify those, and continue to cycle over the expression to simplify further and further. If there are two or more different operators that are each followed by two operands, perform the leftmost operation first. Here's an example:
$\uparrow - * 3 \;7 \;/\; 6 \;2 \;2$$\uparrow - \;21 \;/ \;6 \;2 \;2$$\uparrow - \;21 \;3 \;2$$\uparrow 18 \;2$$324$
Notice that the order that the operands are written in still matters, especially for
division and subtraction! After all, for example, $6 - 2$ is very different from $2 - 6$.
As for post-fix, a similar idea applies except that you would scan the expression for any operators that are preceded by 2 operands. Here's an example:
$3 \;7 * 6 \;2 \;/ - 2 \uparrow$$21 \;6 \;2 \;/ - \;2 \uparrow$$21 \;3 - \;2 \uparrow$$18 \;2 \uparrow$$324$
Converting Between Notations
There are two ways you could convert between in-fix, pre-fix, and post-fix notation. Both are listed down below.
Experiment with both so that you can see which one you prefer more; perhaps you may even use both!
Doing Multiple Scans
Whenever you need to convert in-fix to one of the other two expressions, you can first
list out all of the operands. Then, following the order of operations, slowly add in
all of the operators either before (for pre-fix) or after (for post-fix) the operands
they correspond to. The expression $X = (AB - C/D)\uparrow E$ will be used as an example.
Pre-fix
| Expression | Notes |
|---|---|
$X \; A \; B \; C \; D \; E$ |
We have written out the operands in one row. |
$X * A \; B \; C \; D \; E$ |
$AB$ is one of the first operations to be executed based on PEMDAS; it's located in parentheses and is higher in precedence than subtraction. |
$X * A \; B \; / \; C \; D \; E$ |
$C/D$ is of the same precedence as $AB$ and thus is evaluated next. |
$X - * \; A \; B \; / \; C \; D \; E$ |
$* \; A \; B$ and $/ \; C \; D$ become $AB$ and $C/D$. We then have to find the difference of these two, which is why the subtraction mark is put before both $* \; A \; B$ and $/ \; C \; D$. |
$X \uparrow - * A \; B \; / \; C \; D \; E$ |
$- \; * \; A \; B \; / \; C \; D$ is $(AB - C/D)$, which is supposed to all be taken to the Eth power. So, the $\uparrow$ mark at the front of $- * A \; B \; / \; C \; D$. |
$ = X \uparrow - * A \; B \; / \; C \; D \; E$ |
The equal sign is treated as last in precedence by default since it isn't exactly an operation. |
Post-fix
Notes will not be written for the steps below as they are identical to the steps taken above for pre-fix; the only difference is that the operators are placed after the operands.
$X \; A \; B \; C \; D \; E$$X \; A \; B \; * \; C \; D \; E$$X \; A \; B \; * \; C \; D \; / \; E$$X \; A \; B \; * \; C \; D \; / \; - \; E$$X \; A \; B \; * \; C \; D \; / \; - \; E \; \uparrow$$X \; A \; B \; * \; C \; D \; / \; - \; E \; \uparrow \; =$
On the other hand, if you were to be converting from pre-fix or post-fix to in-fix,
then you could make multiple scans from left to right to convert expressions into
in-fix notation. Parentheses will be helpful for differentiating what you have and have not yet converted. Let's convert the pre-fix expression
from before, $ = X \uparrow - * A \; B \; / \; C \; D \; E$, to better demonstrate
what I mean.
$ = X \uparrow - * A \; B \; / \; C \; D \; E$$ = X \uparrow - \; (AB) \; / \; C \; D \; E$$ = X \uparrow - \; (AB) \; (C/D) \; E$$ = X \uparrow (AB - C/D) \; E$$ = X \; (AB - C/D)\uparrow E$$ X = (AB - C/D)\uparrow E$
If you want to convert from pre-fix to post-fix or vice versa, it is easy to get mixed up; so, converting to in-fix first may be your better choice, although it's a tedious extra step to take. See the next section for a method that will allow for direct conversion from prefix to post fix, but again, just converting to in-fix first is the recommended option.
Binary Trees
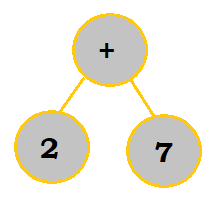
Binary trees are a way to represent an expression more visually. For example, if I
were to represent $3+6$ as a tree, I would draw:
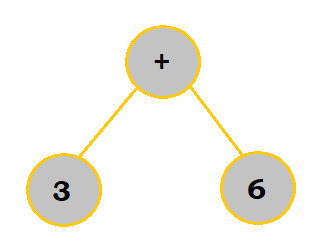
Note how the operator lies in the middle of the two operands and acts as a stem, or root. This applies to even pre-fix and post-fix expressions.
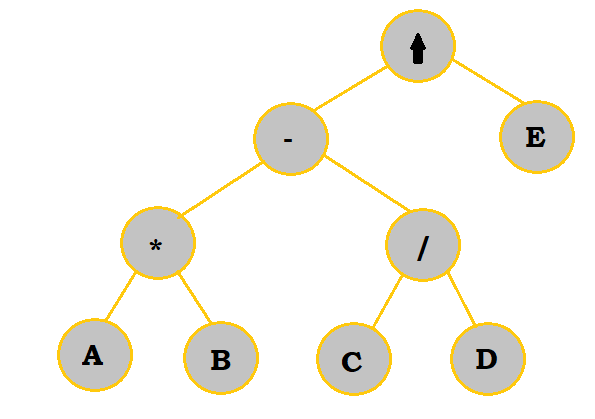
Let's look at $X = (AB - C/D)\uparrow E$ once more and convert it into a tree.
Follow the table below to see the process.
| Construction |
|---|
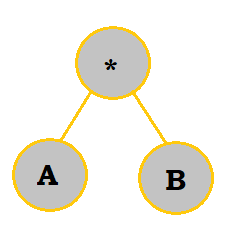 |
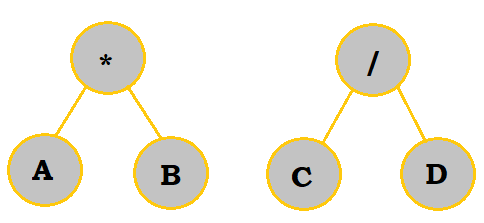 |
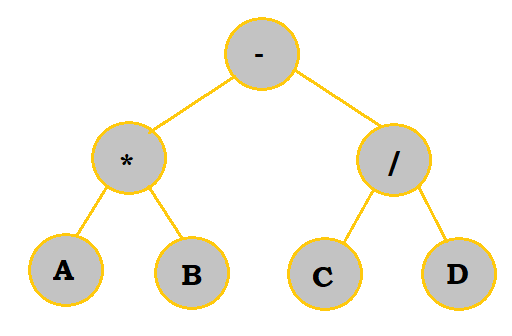 |
 |
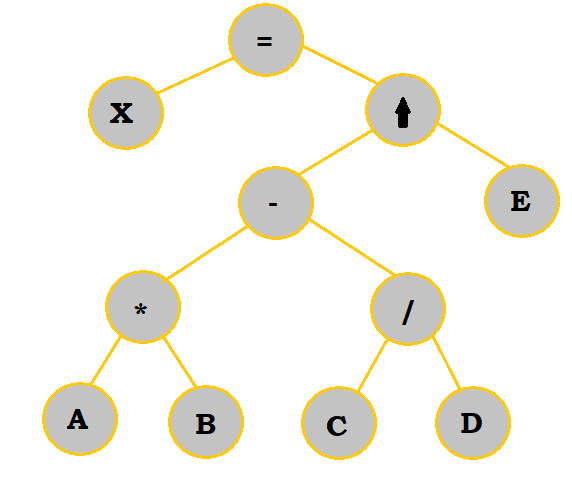 |
Now, with this completed tree, we can convert to any notation we want. The order to
write the expression is already drawn out; first, work with the operation in the
bottommost row on the left (which is $A*B$ in this case). Complete any other
operations in the same row, and then move up to the next row up. In this next row,
start calculating from left to right again before moving up once more. This process
is continued until you get to the uppermost (or final) operation.
Another way to think about converting from a tree to an expression is as follows:
At some point you must visit the parent node, the left child node, and the right child node. Regardless of the notation, start at the parent node.
- For in-fix, follow the simple rule of writing down the left node, the parent node, and then the right node.
- For pre-fix, visit the parent node, the left node, and then the right node.
- For post-fix, visit the left node, the right node, and then the parent node.
If you visit a node's child, and that child has its own child or children, then you would need to analyze that/those 'smaller' child/children first It's quite winding, but hopefully the example below might make some sense.
So for example, let's look back at our tree above and try creating its in-fix representation. We'll start at the root, or the $=$ node.
$=$has a left and right child. Review left child first. -> (nothing written yet)$X$has no children; we will write it down then. ->X- We will write in the
$=$next since that's the parent. ->X = - Review
$=$'s right child now.$\uparrow$has a left and right child. Review left child first. ->X = $-$has a left and right child. Review left child first. ->X =$*$has a left and right child. Review left child first. ->X =$A$has no children. We will proceed to write it down. ->X = A- We will write in the
$*$next because that's just the parent. We will also write in$B$, the right child that also has no children to review. ->X = A * B - We will write in the
$-$from before. Then, we'll analyze its right child,$/$, which has a process similar to steps 6-8. ->X = AB - C / D - We will write in the
$\uparrow$from before. Then, we'll analyze its right child,$E$, which we can just write in because it has no children to analyze first. ->$X = (AB - C/D)\uparrow E$ - There are no other nodes to analyze. Our final expression is
$X = (AB - C/D)\uparrow E$.
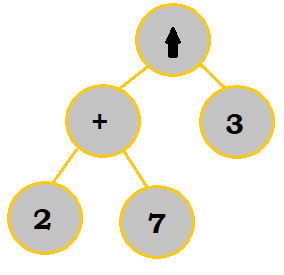
As a recap, the only difference between the notations is where you place the operators. In the binary tree, you may see:

However, since this is written in in-fix terms, you would have to remember to put
the operator before or after the operands if you're converting to pre-fix or post-fix.
So, again, for pre-fix, this would be $* \; A \; B$. For post-fix, it would be
$A \; B \; *$.
Sample Problems
A quick note: for terms that have more than 1 digit, such as 16, parentheses have
been put around them to avoid confusion.
For conversion problems, solutions using both the multiple scans and binary tree methods have been provided.
1. What would the following pre-fix expression evaluate to: $- + * \; 4 \; 6 \; (24) \; / \; 8 \; - * \; 3 \; 2 \; 2$
$- + * \; 4 \; 6 \; (24) \; / \; 8 \; - * \; 3 \; 2 \; 2$$- + \; (24) \; (24) \; / \; 8 \; - * \; 3 \; 2 \; 2$$- \; (48) \; / \; 8 \; - * \; 3 \; 2 \; 2$$- \; (48) \; / \; 8 \; - \; 6 \; 2$$- \; (48) \; / \; 8 \; 4$$- \; (48) \; 2$$46$
2. Convert the following in-fix expression to post-fix: $(2+7)\uparrow 3 - (3+4-5)*8$
Multiple Scans
$2 \; 7 \; 3 \; 3 \; 4 \; 5 \; 8$$2 \; 7 \; + \; 3 \; 3 \; 4 \; 5 \; 8$$2 \; 7 \; + \; 3 \; 3 \; 4 \; + \; 5 \; 8$$2 \; 7 \; + \; 3 \; 3 \; 4 \; + \; 5 \; - \; 8$$2 \; 7 \; + \; 3 \; \uparrow \; 3 \; 4 \; + \; 5 \; - \; 8$$2 \; 7 \; + \; 3 \; \uparrow \; 3 \; 4 \; + \; 5 \; - \; 8 \; *$$2 \; 7 \; + \; 3 \; \uparrow \; 3 \; 4 \; + \; 5 \; - \; 8 \; * \; -$
Binary Tree
(If you didn't know already, you can click on the pictures to see an enlarged view if needed.)
| Construction |
|---|
 |
 |
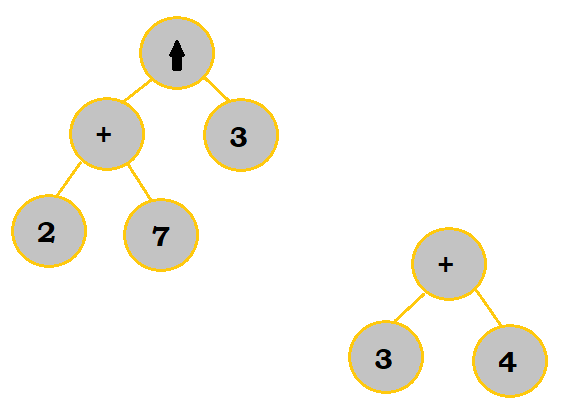 |
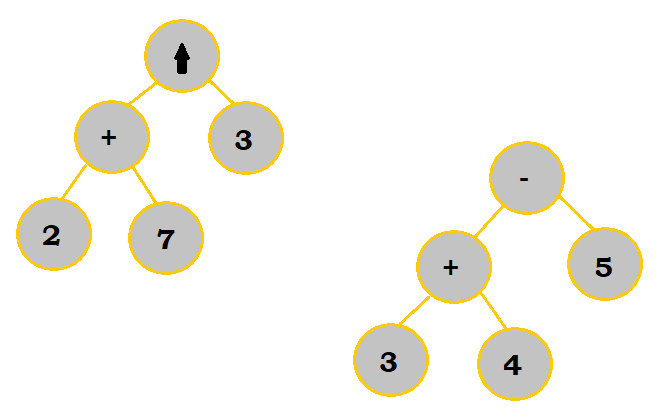 |
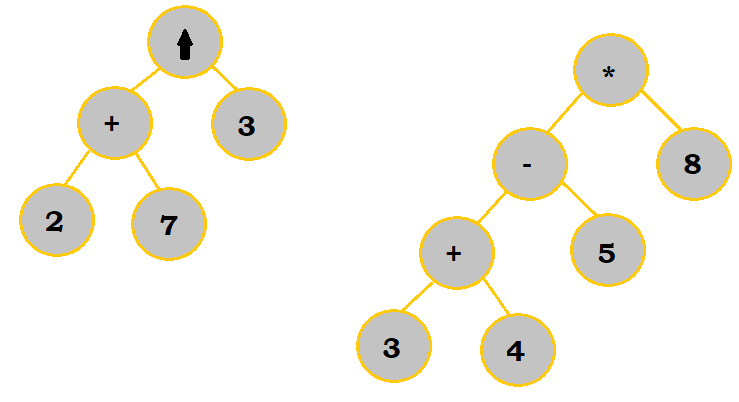 |
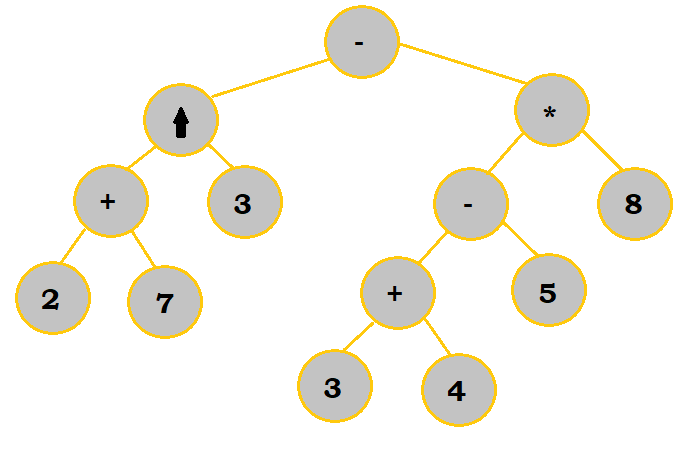 |
Notice that in a few of the steps, I chose to work on subbranches of the final tree before putting them altogether.
Now, at this point, we just need to analyze the tree to get us the post-fix expression we want.
$2 \; 7 \; +$$2 \; 7 \; + \; 3 \; \uparrow$$2 \; 7 \; + \; 3 \; \uparrow$and$3 \; 4 \; +$--> and will be used to divide our conversions into two smaller sections.$2 \; 7 \; + \; 3 \; \uparrow$and$3 \; 4 \; + \; 5 \; -$$2 \; 7 \; + \; 3 \; \uparrow$and$3 \; 4 \; + \; 5 \; - \; 8 \; *$$2 \; 7 \; + \; 3 \; \uparrow \; 3 \; 4 \; + \; 5 \; - \; 8 \; * -$
3. Convert the following post-fix expression to pre-fix: $E \; B \; A \; C \; + / \; D \; - \uparrow$
Multiple Scans
First, we will convert the post-fix expression to in-fix:
$E \; B \; A \; C \; + / \; D \; - \uparrow$$E \; B \; (A+C) \; / \; D \; - \uparrow$$E \; (B \; / \; (A+C)) \; D \; - \uparrow$$E \; (B \; / \; (A+C) \; - \; D) \; \uparrow$$E \; \uparrow (B \; / \; (A+C) \; - \; D)$
Then, we will convert this into pre-fix:
$E \; B \; A \; C \; D$$E \; B \; + \; A \; C \; D$$E \; / \; B \; + \; A \; C \; D$$E \; - / \; B \; + \; A \; C \; D$$\uparrow \; E \; - / \; B \; + \; A \; C \; D$
Binary Tree
We would first construct the tree like so:
| Construction |
|---|
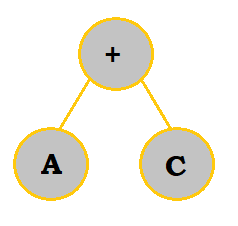 |
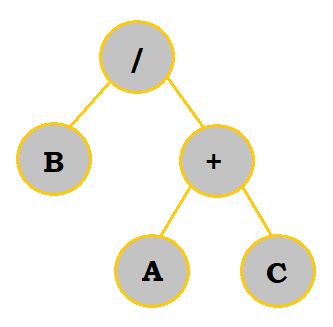 |
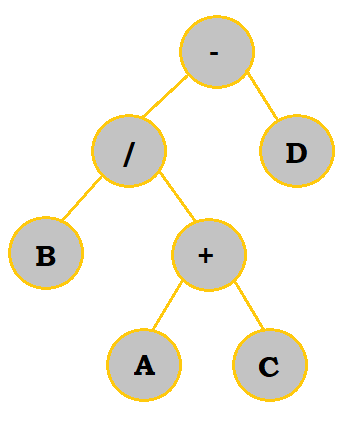 |
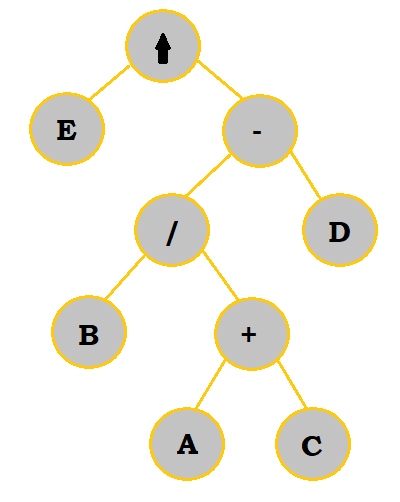 |
Then, we can analyze this tree from bottom to top, left to right to get our pre-fix expression:
$+ \; A \; C$$/ \; B \; + \; A \; C$$- \; / \; B \; + \; A \; C \; D$$\uparrow \; E \; - / \; B \; + \; A \; C \; D$
Author: Kelly Hong